Backtracking Algorithm

Hi! This is Harshit Sharma, a B.Tech. computer science undergrad student from Bennett University. In the current semester we have a subject called Design and analysis of algorithm, and while exploring some resources on this subject, I came across an interesting algorithm technique called, back tracking.

What is algorithm?

• Algorithm basically refers to the method of processing data stored in various data structure, to produce a desired and efficient output.
• Or we can say it is finite set of instructions that are carried in a specific order to perform a specific task.
• E.g.- Sorting, searching, etc.

Introduction to backtracking.

Backtracking is an algorithmic-technique for solving problems recursively by trying to build a solution incrementally, one piece at a time.

It uses brute force approach. This we were already doing in dynamic programming, but using dynamic programming we solve optimization problem and back tracking is not dynamic its about picking up all the possible solutions then choosing the desired solution.

Generally the desired solution is chosen on the basis of some constraint, It removes those solutions that fail to satisfy the constraints of the problem at any point of time.

Now, to have a clear understanding if backtracking and how it uses brute force, lets look at an example.

Suppose if there are three students 2 boys and a girl and there are three chairs and we have to arrange them in those chairs.

Total ways — 3!

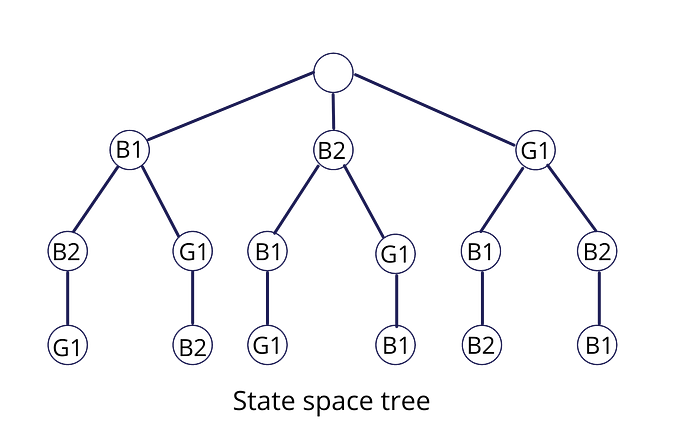
Now, lets add a constraint, that a girl cannot sit in middle.

So, we’ll retrace and draw the tree again.

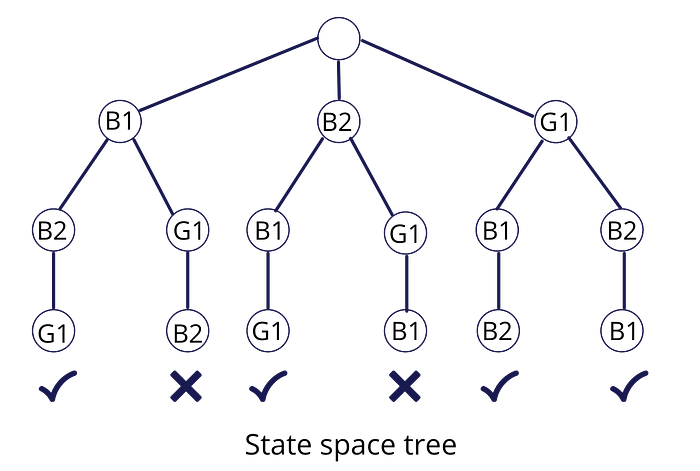
Now, the tree will look like:

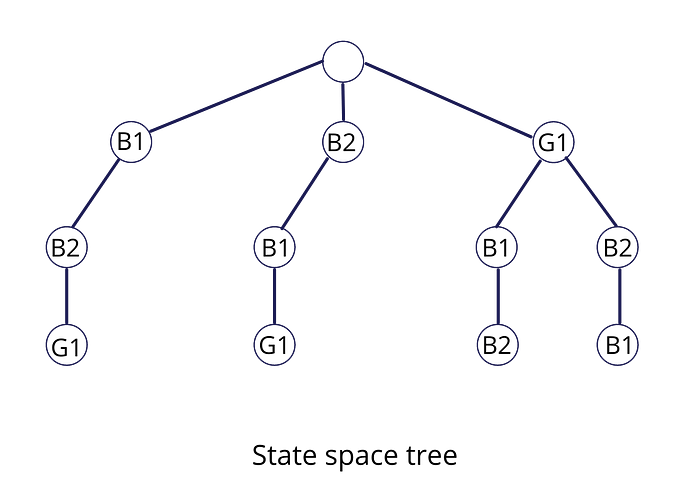
So, I hope that the basic concept of backtracking and how it uses brute force is clear after this example.

And now we can move on to its applications:

Applications of backtracking:

• N queen problem.
• M coloring problem.
• Hamiltonian cycle.
• Rat in a maze.

N-Queen problem

Problem:

The N Queen is the problem of placing N chess queens on an N×N chessboard so that no two queens attack each other.

Approach:

There are three constraints:

• Rows should not be the same.
• Column should not be the same .
• Should not be in diagonal.

Now, we look at the first two constraint and draw the state space tree.

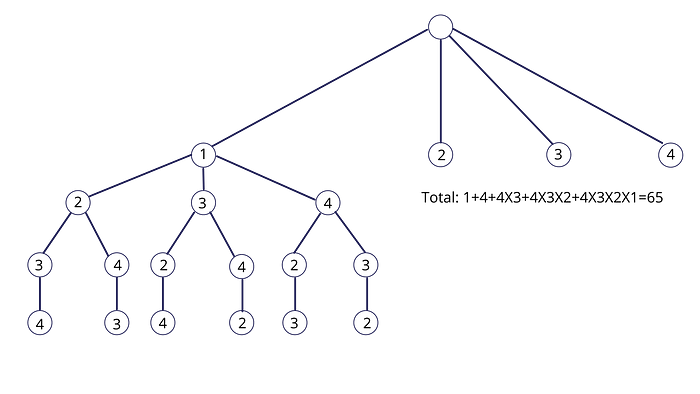
Now, let’s focus on the 3rd constraint and back track the state space tree to discard the non satisfying nodes.

We have discarded all the diagonal position nodes.

Moving ahead in similar way we’ll place queen one on the second block and then draw the same tree again.

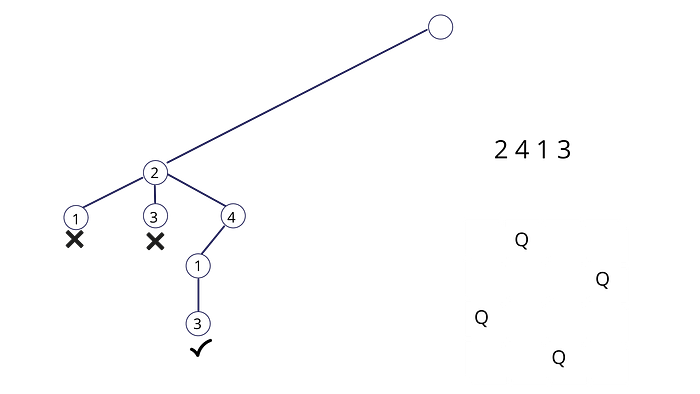
which is our required solution.

Code:

#define N 4

#include <stdbool.h>

#include <stdio.h>

void printSolution(int board[N][N])

{

for (int i = 0; i < N; i++) {

for (int j = 0; j < N; j++)

printf(“ %d “, board[i][j]);

printf(“\n”);

}

}

bool isSafe(int board[N][N], int row, int col)

{

int i, j;

for (i = 0; i < col; i++)

if (board[row][i])

return false;

for (i = row, j = col; i >= 0 && j >= 0; i — , j — )

if (board[i][j])

return false;

for (i = row, j = col; j >= 0 && i < N; i++, j — )

if (board[i][j])

return false;

return true;

}

bool solveNQUtil(int board[N][N], int col)

{

if (col >= N)

return true;

for (int i = 0; i < N; i++) {

if (isSafe(board, i, col)) {

board[i][col] = 1;

if (solveNQUtil(board, col + 1))

return true;

board[i][col] = 0; // BACKTRACK

}

}

return false;

}

bool solveNQ()

{

int board[N][N] = { { 0, 0, 0, 0 },

{ 0, 0, 0, 0 },

{ 0, 0, 0, 0 },

{ 0, 0, 0, 0 } };

if (solveNQUtil(board, 0) == false) {

printf(“Solution does not exist”);

return false;

}

printSolution(board);

return true;

}

// driver program to test above function

int main()

{

solveNQ();

return 0;

}

Output:

 0  0  1  0 
 1  0  0  0 
 0  0  0  1 
 0  1  0  0

Pros:

1. Easy to implement.
2. Easy to code.
3. Used to find all the existing solution if there exist for any problem.

Cons:

1. Very time inefficient.
2. Large space complexity.